Image Segmentation Model¶

This notebook is an example of training a UNet-based image segmentor in Kokoyi, and is an example of mapping a tensor (an image in $\mathbb{R}^3$) to another (the segmentation mask $\mathbb{R}^2$).

UNet¶

UNet is a convolutional neural network that was developed for biomedical image segmentation at the Computer Science Department of the University of Freiburg. The network is based on the fully convolutional network and its architecture was modified and extended to work with fewer training images and to yield more precise segmentations.

The UNet consists of a contracting path and an expansive path. The contracting path follows the typical architecture of a convolutional network. It consists of the repeated application of two 3x3 convolutions (unpadded convolutions), each followed by a rectified linear unit (ReLU) and a 2x2 max pooling operation with stride 2 for downsampling.

Every step in the expansive path consists of an upsampling of the feature map followed by a 2x2 convolution (“up-convolution”) that halves the number of feature channels, a concatenation with the correspondingly cropped feature map from the contracting path, and two 3x3 convolutions, each followed by a ReLU. The cropping is necessary due to the loss of border pixels in every convolution. At the final layer a 1x1 convolution is used to map each feature vector to the desired number of classes.

UNet

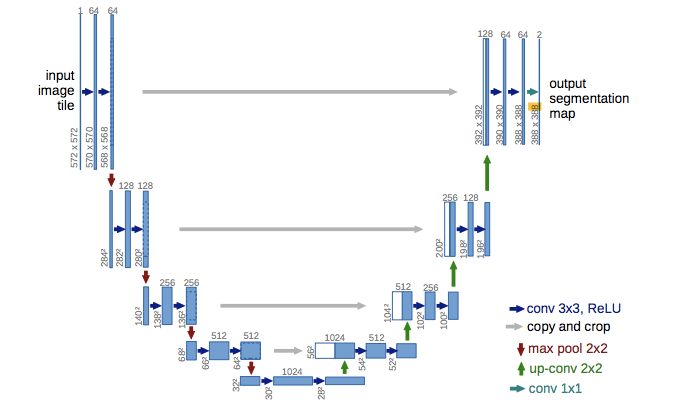
Following the architecture above, this can be very succinctly described in Kokoyi.

\Module {UNet} {x; ConvBlock, Downs, Ups, Conv2d}
    L \gets |Downs| \\
    h^d[0 \leq l \leq L] \gets \begin{cases}
        ConvBlock(x) & l = 0 \\
        Downs[l - 1](h^d[l - 1]) & l \leq L
    \end{cases} \\

    h^u[0 \leq l \leq L - 1] \gets \begin{cases}
        Ups[0](h^d[L], h^d[L - 1]) & l = 0 \\
        Ups[l](h^u[l - 1], h^d[L - 1 - l]) & l < L
    \end{cases}  \\
    
    \Return Conv2d(h^u[L - 1]) \\
\EndModule

Next, we will describe the 3 modules needed.

The $ConvBlock$ module has been introduced in the MLP_CNN notebook. If interested, you can find more useful Functions and Modules in Kokoyi Gallery.

\Module {ConvBlock}{x ; Conv2d_0, Conv2d_1} 
    \Return \ReLU(Conv2d_1(\ReLU(Conv2d_0(x)))) \\
\EndModule

The $Down$ module first applies MaxPool2d function to the input and then applies the $ConvBlock$ submodule.

\Module{Down}{x ; ConvBlock}
    \Return ConvBlock(\MaxPool2d(x, 2)) \\
\EndModule

The $Up$ module first applies a bilinear upsample on the 2D-input $x$, and then pads it to the shape of $y$. The padded result $u$ will be concatenated with $y$. The $ConvBlock$ submodule is used to merge the information from $x$ and $y$.

\Module {Up}  {x, y ; Upsample, ConvBlock}
    u \gets Upsample(x) \\
    h \gets y || u \\
    \Return ConvBlock(h) \\
\EndModule

You can write the completed module definitions in the following code cell, or you can use auto-init feature.

Click here

to see the default initialization code generated by Kokoyi for this model.

class ConvBlock(torch.nn.Module):
    def __init__(self):
        """ Add your code for parameter initialization here (not necessarily the same names)."""
        super().__init__()
        self.Conv2d_0 = None
        self.Conv2d_1 = None

    def get_parameters(self):
        """ Change the following code to return the parameters as a tuple in the order of (Conv2d_0, Conv2d_1)."""
        return None

    forward = kokoyi.symbol["ConvBlock"]

class Down(torch.nn.Module):
    def __init__(self):
        """ Add your code for parameter initialization here (not necessarily the same names)."""
        super().__init__()
        self.ConvBlock = None

    def get_parameters(self):
        """ Change the following code to return the parameters as a tuple in the order of (ConvBlock)."""
        return None

    forward = kokoyi.symbol["Down"]

class Up(torch.nn.Module):
    def __init__(self):
        """ Add your code for parameter initialization here (not necessarily the same names)."""
        super().__init__()
        self.Upsample = None
        self.ConvBlock = None

    def get_parameters(self):
        """ Change the following code to return the parameters as a tuple in the order of (Upsample, ConvBlock)."""
        return None

    forward = kokoyi.symbol["Up"]

class UNet(torch.nn.Module):
    def __init__(self):
        """ Add your code for parameter initialization here (not necessarily the same names)."""
        super().__init__()
        self.ConvBlock = None
        self.Downs = None
        self.Ups = None
        self.Conv2d = None

    def get_parameters(self):
        """ Change the following code to return the parameters as a tuple in the order of (ConvBlock, Downs, Ups, Conv2d)."""
        return None

    forward = kokoyi.symbol["UNet"]

You may have noticed that we use kokoyi.nn.Conv2d instead of torch.nn.Conv2d, the same goes for the Upsample module. This is a concept explained in MLP_CNN notebook notebook but worth repeating here: NN modules in Kokoyi are basically the same as NN modules in torch; Kokoyi only makes changes inside the forward function for auto-batching. So please feel free to set up a kokoyi module with the same parameters used in torch.

class ConvBlock(torch.nn.Module):
    def __init__(self, in_channels, out_channels, mid_channels=None):
        super().__init__()
        if not mid_channels:
            mid_channels = out_channels
        self.conv0 = kokoyi.nn.Conv2d(in_channels, mid_channels, 3, 1, 1)
        self.conv1 = kokoyi.nn.Conv2d(mid_channels, out_channels, 3, 1, 1)

    def get_parameters(self):
        return self.conv0, self.conv1

    forward = kokoyi.symbol["ConvBlock"]


class Down(torch.nn.Module):
    def __init__(self, in_channels, out_channels):
        super().__init__()
        self.convblock = ConvBlock(in_channels, out_channels)

    def get_parameters(self):
        return self.convblock

    forward = kokoyi.symbol["Down"]


class Up(torch.nn.Module):
    def __init__(self, in_channels, out_channels, out_shape):
        super().__init__()
        self.Upsample = kokoyi.nn.Upsample((out_shape, out_shape), mode='bilinear')
        self.ConvBlock = ConvBlock(in_channels, out_channels, in_channels // 2)

    def get_parameters(self):
        return self.Upsample, self.ConvBlock

    forward = kokoyi.symbol["Up"]


class UNet(torch.nn.Module):
    def __init__(self, n_channels, n_classes):
        super().__init__()
        self.inc = ConvBlock(n_channels, 64)
        self.downs = torch.nn.ModuleList([
            Down(64, 128),
            Down(128, 256),
            Down(256, 512),
            Down(512, 512),
        ])
        self.ups = torch.nn.ModuleList([
            Up(1024, 256, int(380/2/2/2)),
            Up(512, 128, int(380/2/2)),
            Up(256, 64, int(380/2)),
            Up(128, 64, 380),
        ])
        self.outConv = kokoyi.nn.Conv2d(64, n_classes, 1)

    def get_parameters(self):
        return self.inc, self.downs, self.ups, self.outConv

    forward = kokoyi.symbol["UNet"]

Loss. We use the binary cross entropy loss( torch.nn.BCEWithLogitsLoss ):

loss(\hat{y}, y) \gets \BCELossWithLogits(\hat{y}, y) \\

Image segmentation using UNet¶

Let's first do some setup:

import os
import random
import kokoyi
import numpy as np
import torch
import torch.nn as nn
from torch import optim
from torch.utils.data import DataLoader
from torchvision.datasets import VOCSegmentation
import torchvision.transforms as transforms

We will use the Pascal VOC Segmentation Dataset in torchvision. The dataset consists of several images and their pixel-wise segmentations.

batch_size = 4

transform = transforms.Compose([
    transforms.Resize(400),
    transforms.CenterCrop(380),
    transforms.RandomHorizontalFlip(),
    transforms.ToTensor()
])

train_dataset = VOCSegmentation(root='data/', image_set='train', year='2011', 
                                transform=transform, 
                                target_transform=transform, download=True)
test_dataset = VOCSegmentation(root='data/', image_set='val', year='2011', 
                                transform=transform, target_transform=transform)
train_dataloader = DataLoader(
    train_dataset,
    batch_size=batch_size,
    shuffle=True
)
test_dataloader = DataLoader(
    test_dataset,
    batch_size=batch_size,
    shuffle=False
)

# Use GPU if possible
if torch.cuda.is_available():
    device_name = 'cuda'
else:
    device_name = 'cpu'
print('Using device: ', device_name)
device = kokoyi.Config.device = torch.device(device_name)

Finally, we can set the hyper-parameters and start training!

net = UNet(n_channels=3, n_classes=1).to(device)
optimizer = optim.RMSprop(net.parameters(), lr=0.0001, weight_decay=1e-8, momentum=0.9)

for epoch in range(3):
    epoch_loss = 0
    total_correct = 0
    total_label = 0
    for step, data in enumerate(train_dataloader):
        images, targets = data
        images = images.to(device=device, dtype=torch.float32)
        true_masks = targets.to(dtype=torch.long).to(device=device, dtype=torch.float32)
        
        # zero the parameter gradients
        optimizer.zero_grad()
        
        # forward
        masks_pred = net(images, batch_level=[1])
        
        loss = kokoyi.symbol["loss"](masks_pred, true_masks, batch_level=[1,1])
        loss.backward()
        optimizer.step()
        nn.utils.clip_grad_value_(net.parameters(), 0.1)
        
        epoch_loss += loss.item()
        total_correct = masks_pred
        print("Batch {}: loss {}".format(step, loss.item()))

    print("Epoch {}: loss {}".format(epoch, epoch_loss))